Anna University
Department of Electrical and Electronics Engineering
CE 2252 / STRENGTH OF MATERIALS QUESTION BANK – 2013 Edition
DEPARTMENT: CIVIL
SEMESTER: IV
SUBJECT CODE / Name: CE 2252 / STRENGTH OF MATERIALS
UNIT – I - ENERGY PRINCIPLES
PART – A (2 Marks)
1. A beam of span 4 m is cantilever and subjected to a concentrated load 10 kN at free end. Find the total strain energy stored. Take the Flexural rigidity is EI.
(AUC Apr/May 2010)
2. Write down Maxwell’s reciprocal theorem. (AUC Apr/May 2010)
3. Write down the expression for strain energy stored in a bar of cross sectional area A
and length ‘l’ and subjected to a tensile load ‘W’. (AUC Nov/Dec 2010)
4. State Maxwell’s reciprocal theorem. (AUC Nov/Dec 2010, Apr/May 2011 & 2012)
5. State the principle of virtual work. (AUC Apr/May 2011)
6. Calculate the strain energy stored in the beam shown in fig. EI constant.
7. State Castigliano’s first theorem. (AUC Nov/Dec 2011)
8. Find the deflection at free end of the cantilever of 1m span carrying a point load of 10kN
at free end. EI=25000kNm2 using principle of virtual work. (AUC Apr/May 2012)
9. Define strain energy density.
10. Define proof resilience.
11. Define the terms: Proof resilience and Modulus of resilience.
12. Derive relation for strain energy due to shear.
13. Define the term Poisson’s ratio and Bulk modulus.
14. Explain the effect of change of temperature in a composite bar.
15. What is meant by Strain energy?
16. Write down the equilibrium equations?
17. Define modulus of resilience.
18. Define unit load method.
19. Write down the different typed of loads due to different stresses?
20. Compare the unit load method and Castigliano’s first theorem
PART – B (16 Marks)
1. For the beam shown in Fig, find the deflection at C and slope at D (AUC Apr/May 2010)
I = 40 x 107 mm4
E = 200 GPa.
2. For the truss shown in Fig, find the horizontal movement of the roller at D AB, BC, CD area = 8 cm2 (AUC Apr/May 2010) AD and AC = 16 cm2
E = 2 x105 N / mm2.
3. Derive the expression for strain energy in Torsion of a circular shaft of length ‘I’ and radius ‘R’ subjected to a Torque ‘T’ producing a twist ‘ θ ’ in the length of the shaft for the following cases. (AUC Nov/Dec 2010) (i) Solid circular shaft and
(ii) Hollow circular shaft, with an external radius ‘R’ and internal radius ‘r’.
4. i) An axial pull of 40 kN is suddenly applied to a steel rod 2m long and 1000mm2 in cross section. Calculate the strain energy that can be absorbed if E = 200 GN/m2.
ii) A cantilever of rectangular section breadth b, depth d and of length l carries uniformly distributed load spread from free end to the mid section of the cantilever. Using Castigliano’s theorem find: Slope and deflection due to bending at the free end. (AUC Nov/Dec 2010)
5. A beam 4m in length is simply supported at the ends and carries a uniformly distributed load of 6 kN/m length. Determine the strain energy stored in the beam. Take E = 200 GPa and I = 1440 cm4. (AUC Apr/May 2011)
6. A beam simply supported over a span of 3m carries a UDL of 20 kN/m over the entire span. The flexural rigidity EI = 2.25 MNm2 Using Castigliano’s theorem, determine the deflection at the centre of the beam. (AUC Apr/May 2011)
7. For the beam shown in fig. find the slope and deflection at ‘C’. (AUC Nov/Dec 2011)
8. i) For the truss shown in fig. find the total strain energy stored. (AUC Nov/Dec 2011)
| |
Area : AB : 100 mm2
BC : 100 mm2
AC : 80 mm2
ii) For the truss shown in fig. find the vertical deflection at ‘C’. (AUC Nov/Dec 2011)
| |
all the members : 100 mm2
E = 2 × 105 N/mm2
9. Determine vertical and horizontal deflection of joint C as shown in fig. Using principle of virtual work. Take E=200kN/mm2 and A=600mm2 for all the members.
(AUC Apr/May 2012)
10. Using Castigliano’s theorem, find the slope and deflection at B for the cantilever beam
shown in fig. Take E=2 x 105 N/mm2 and I = 1 x 108 mm4. (AUC Apr/May 2012)
11. i. Derive a relation for strain energy due to shear force. (4m)
ii. Derive a relation for maximum deflection of a simply supported beam with uniformly distributed load over entire span. Use strain energy method. (12m)
12. Determine the deflection at C of the beam given in Fig. Use principal of virtual work.
13. The external diameter of a hollow shaft is twice the internal diameter. It is subjected to pure torque and it attains a maximum shear stress ‘τ’. Show that the strain energy stored
per unit volume of the shaft is
16C
. Such a shaft is required to transmit 5400 kw at 110
r.p.m. with uniform torque, the maximum stress not exceeding 84 MN/m2. Determine i. The shaft diameters (8m)
ii. The strain energy stored per m3. Take C = 90 GN/m2. (8m)
13. Using Castigliano’s theorem, determine the deflection of the free end of the cantilever beam shown in fig. A is fixed and B is free end Take EI = 4.9 MN/m2
15. A beam 4m in length is simply supported at the ends and carries a UDL of 6 kN/m length over the entire length. Determine the strain energy stored in the beam. Take E = 200
GN/m2 and I = 1440 cm4.
16. A beam simply supported over a span of 3m carries a UDL of 20 kN/m over the entire span. Taking EI = 2.25 MNm2 and using Castigliano’s theorem, determine the deflection at the centre of the beam.
17. A continuous beam of two equal spans L is uniformly loaded over its entire length. Find
the magnitude R of the middle reaction by using Castigliano’s theorem.
18. Determine the vertical displacements of both lower points C and D for the pin jointed frame shown in fig. The cross sectional area of all members is 130mm2 and the modulus of elasticity is 200 kN/mm2. Determine the magnitude of an additional vertical load placed at D necessary to increase the deflection at C by 50%.
19. A simply supported beam of span “l” carries an uniformly distributed load of w per unit
length over the entire span. Using Castigliano’s theorem determine
i. The mid-span deflection of the beam ii. The slope at the left support.
20. A simply supported beam of span 8 m carries two concentrated loads of 20 kN and 30 kN at 3 m and 6 m from left support. Calculate the deflection at the centre by strain energy principle.
21. Using Castigliano’s theorem, determine the deflection of the free end of the cantilever
beam shown in fig. A is fixed and B is free end. Take EI = 4.9 MNm2.
22. The external diameter of a hollow shaft is twice the internal diameter. It is subjected to pure torque and it attains a maximum shear stress ‘τ’. Show that the strain energy stored per unit volume of the shaft is 5 τ2 / 16C. Such a shaft is required to transmit 5400 kw at
110 r.p.m. with uniform torque, the maximum stress not exceeding 84 MN / m2.
Determine,
i. The shaft diameter (8m)
ii. The strain energy stored per m3. Take C = 90 GN / m2. (8m)
23. State and prove Maxwell’s reciprocal theorem.
24. State and prove Castigliano’s theorem.
25. Find the deflection at the mid span of a simply supported beam carrying an UDL of 5 kN/m over the entire span using principle of virtual work. Take span = 5m.
UNIT – II - INDETERMINATE BEAMS
PART – A (2 Marks)
1. A fixed beam of span ‘L’ is subjected to UDL throughout w/m. What is end moments and moment at the centre? (AUC Apr/May 2010)
2. Draw BMD for a propped cantilever beam span ‘L’ subjected to UDL throughout w/m.
(AUC Apr/May 2010)
3. Draw BM Diagram (qualitative) of a propped cantilever of L m long carries an UDL of w/unit run over the entire span. (AUC Nov/Dec 2010)
4. Draw the SF and BM Diagrams (qualitative) of a fixed beam of L m long carries a point load W at the midpoint. (AUC Nov/Dec 2010)
5. What is a fixed beam? (AUC Apr/May 2011)
6. State theorem of three moments. (AUC Apr/May 2011)
7. For the fixed beam shown in fig. what is the fixed end moment at A and B.
8. For the propped cantilever shown in fig. draw the BMD (qualitative).
9. Write down the three moment equations for a fixed beam carrying an UDL of 2 kN/m over the entire span. Span = 4m. (AUC Apr/May 2012)
10. State any two methods of analysis of indeterminate beams. (AUC Apr/May 2012)
11. A cantilever of length 6m carries a point load of 48 kN at its centre. The cantilever is propped rigidly at the free end. Determine the reaction at the rigid prop.
12. A fixed beam AB of length 3m is having moment of inertia I=3 x 106 mm4 the support B
sinks down by 3mm. If E = 2 x 105 N/mm2. Find the fixing moments.
13. What do you understand by bucking load and safe load?
14. What are the assumptions made in Euler’s theory?
15. What are the fixed end moments for a fixed beam of length l subjected to a concentrated load W at a distance a from left end.
16. State theorem of three moments.
17. What do you mean by a fixed beam?
18. How will you apply clapeyron’s theorem of three moments to a continuous beam with
fixed end supports?
19. Derive a relation fro prop reaction for a simply supported beam with uniformly distributed load and propped t the centre.
20. A Steel fixed beam AB of span 6 m is 60 mm wide and 100 mm deep. The support B
sinks down by 6 mm. Fine the fixing moments at A and B. Take E = 200 GPa.
21. Sketch the bending moment diagram of a cantilever beam subjected o udl over the entire span.
22. What is meant by point of contraflexure?
23. A cantilever beam 4 m long carries a load of 20 kN at its free end. Calculate the shear force and bending moment at the fixed end.
24. What are the advantages and disadvantages of a fixed beam?
25. Define continuous beam?
26. Define flexural rigidity of beams?
27. What is meant by propped cantilever?
28. Write down the general form of clapeyron’s three moment equations for the continuous
beam?
PART – B (16 Marks)
1. For the fixed beam shown in Fig, draw the SFD and BMD. (AUC Apr/May 2010)
2. For the continuous beam shown in Fig, draw SFD and BMD all the supports are at same level. (AUC Apr/May 2010)
3. A fixed beam AB of 4.5m span carries a point load of 80 kN at its mid span and a uniformly distributed load of 15 kN/m throughout its entire span. Find the following:
(i) Fixing moments at the ends and
(ii) Reactions at the supports
Also draw the SF and BM diagrams. (AUC Nov/Dec 2010)
4. A continuous beam ABCD of uniform cross-section is loaded as shown in Figure Find the following: (AUC Nov/Dec 2010) (i) Bending moments at the supports
(ii) Reactions at the supports.
Also draw BM and SF diagrams.
5. A fixed beam of 6m span is loaded with point loads of 150 kN at distance of 2m from each support. Draw the bending moment diagram and shear force diagram. Also find the maximum deflection. Take E = 200GPa and I = 8 × 108 mm4. (AUC Apr/May 2011)
6. A continuous beam consists of three successive spans of 6 m, 12 m and 4 m and carries loads of 2 kN/m, 1 kN/m and 3 kN/m respectively on the spans. Draw bending moment diagram and shear force diagram for the continuous beam. (AUC Apr/May 2011)
7. A fixed beam AB is 6 m span and carries a point load 10 kN at 1 m from left end. It also carries a clockwise moment at 1 m from right end,10 kN/m. Draw SFD and BMD indicating the salient points. (AUC Nov/Dec 2011)
8. A continuous beam ABCD in shown in Fig. Draw SFD and BMD indicating the salient points. (AUC Nov/Dec 2011)
9. Draw the S.F. and B.M. diagrams for the beam shown in the fig. (AUC Apr/May 2012)
10. Draw the S.F. and B.M. diagrams for the beam shown in the fig. Use three moment equation. (AUC Apr/May 2012)
11. A simply supported beam of span 10m carries a UDL of 1152 N per unit length. The beam is propped at the middle of the span. Find the amount by which the prop should yield, in order to make all the three reactions equal. Take E=2 x 105 N/mm2 and I for beam= 106 mm4.
12. A fixed beam AB of length 6m carries point loads of 160 kN and 120kN at a distance of
2m and 4m from the left end A. Find the fixed end moments and the reactions at the supports. Draw BM and SF diagrams.
13. A fixed beam of 8m span carries a UDL of 40 kN/m run over 4m length starting from left end and a concentrated load of 80kN at a distance of 6m from the left end. Find
i. Moments at the supports. (12m)
ii. Deflection at centre of the beam (4m)
Take EI = 15000 kNm2.
12. A cantilever AB of span 6m is fixed at the end ‘A’ and propped at the end B. It carries a point load of 50 kN at the mid span. Level of the prop is the same as that of the fixed end.
i. Determine reaction at the prop. (12m)
ii. Draw the S.F. and B.M. diagrams. (4m)
14. A fixed beam of 6m length is loaded with two equal point loads of 150kN each at distance of 2m from each support. Draw the BMD and SFD. E = 2 x 108 kN/m2, I = 8 x 108 mm4.
15. A continuous beam ABC 8m long consists of two spans AB = 3m and BC = 5m. The span AB carries a load of 50 kN/m while the span BC carries a load of 10 kN/m. Find the support moments and the reactions at the supports.
16. A fixed beam of span 8 m carries an udl of 2 kN/m over a length of 4 m from the left support and a concentrated load of 10 kN at a distance of 6m from the left support. Find the fixed end moments and draw the B.M. and S.F. diagrams.
17. A propped cantilever of span of 10m having the prop at the end is subjected two concentrated loads of 15KN and 30KN at one third points respectively from left fixed end support. Draw SFD and BMD.
18. Analyse the following beam.
UNIT – III - COLUMNS PART – A (2 Marks)
1. Define core of a section and draw the same for a circular section. (AUC Apr/May 2010)
2. Write Rankine’s equation for column. (AUC Apr/May 2010)
3. Define: Eccentrically loaded short columns. (AUC Nov/Dec 2010)
4. Distinguish between thick and compound cylinders. (AUC Nov/Dec 2010)
5. How columns are classified depending upon slenderness ratio? (AUC Apr/May 2011)
6. What is thick cylinder? (AUC Apr/May 2011)
7. State any two assumptions made in the derivation of Euler’s formula for long columns. (AUC Nov/Dec 2011)
8. Define ‘core’ of a section. (AUC Nov/Dec 2011)
9. What is the buckling load of an Euler’s column 100mm x 200mm fixed at both the ends
and length is 5m. Take E=200kN/mm2? (AUC Apr/May 2012)
10. Write down the Rankine-Gordon formula. (AUC Apr/May 2012)
11. State middle third rule.
12. How is the failure of thick cylinder different from that of a thin cylinder?
13. Write down the Lame’s equations for thick walled cylinder.
14. What are the advantages of continuous beams over simply supported beams?
15. What are the assumptions made in Euler’s theory?
16. Define slenderness ratio of a column.
17. How the failure of a short and of a long column takes place?
18. How will you determine the hoop stress in a thick compound cylinder?
19. Express the strength of a solid shaft.
20. Differentiate a thin cylinder and a thick cylinder with respect to hoop stress.
21. Discuss the effect of crippling load (Pc) obtained by Euler’s formula on Rankine’s formula for short columns.
22. Give the expression for finding deflection of closely coiled helical spring.
23. Give the equivalent length of a column for any two end conditions.
24. Write down Rankine-Gordon formula for eccentrically loaded columns.
25. Define buckling.
26. Define critical load.
27. What is beam column?
PART – B (16 Marks)
1. i) Derive the Euler’s equation for column with two ends fixed. (AUC Apr/May 2010) ii)A circular bar of uniform section is loaded with a tensile load of 500 kN. The line of action of the load is off the axis of the bar by 10 mm. Determine the diameter of
the rod, if permissible stress of the material of the rod is 140 N / mm2.
(AUC Apr/May 2010)
2. Find the greatest length of a mild steel rod of 30 mm × 30 mm which can be used as a compressive member with one end fixed and the other end hinged. It carries a working
1
load of 40 kN. Factor of safety = 4, α =
and σc = 300N / mm2.
Compare the result
with Euler. E = 2 ×105 N / mm2. (AUC Apr/May 2010)
3. i) What are the assumptions and limitations of Euler’s theory for long columns?
ii) A slender pin ended aluminium column 2.0 m long and of circular cross section it to have an outside diameter of 50 mm. Calculate the necessary internal diameter to prevent failure by buckling if the actual load applied is l2kN and the critical load applied is twice the actual load. Take E for aluminium as 70 GN/m2.
(AUC Nov/Dec 2010)
4. i) Describe the Rankine’s method for columns subjected to Eccentricity.
ii) From the following data of a column of circular section calculate the extreme stresses on the column section. Also find the maximum eccentricity in order that there may be no tension anywhere on the section.
External diameter = 20 cm Internal diameter = 6 cm Length of the column = 4 m
Load carried by the column = 175 kN
Eccentricity of the load = 2.5 cm (from the axis of the column) End conditions = Both ends fixed
Young’s modulus = 94 GN/m2. (AUC Nov/Dec 2010)
5. A 1.5m long cast iron column has a circular cross section of 50mm diameter.
One end of the column is fixed in direction and position and the other is free. Taking factor of safety as 3, calculate the safe load using Rankine-Gordon formula. Take yield stress as 560 MPa and constant α = 1/1600. (AUC Apr/May 2011)
6. A pipe of 200mm internal diameter and 50mm thickness carries a fluid at a pressure of
10 MPa. Calculate the maximum and minimum intensities of circumferential stress across the section. Also sketch the radial stress distribution and circumferential stress distribution across the section. (AUC Apr/May 2011)
7. i) A rectangular strut is 25 cm × 15 cm. It carries a load of 60 kN at an eccentricity of 2 cm in a plane bisecting the thickness. Find the minimum and maximum stresses developed in the section.
ii) Derive the Euler’s equation for a long column with both ends hinged.
(AUC Nov/Dec 2011)
8. i) A hollow cylindrical cast iron column is 3.50 long with both ends fixed. Determine the minimum diameter of the column if it has to carry a safe load of 300 kN with a factor of safety 4. External diameter is 1.25 times the internal diameter. a = 1/1600, σc = 550
MN/m2, in Rankine’s formula. (AUC Nov/Dec 2011)
ii) Define ‘thick cylinder’ and draw the hoop stress distribution for a solid circular cylinder.
(AUC Nov/Dec 2011)
9. Derive the expression for the buckling load of an Euler’s column fixed at one end and
hinged at the other end. (AUC Apr/May 2012)
10. A short length of a tube of 60mm external diameter and with thickness 5mm, failed in compression at a load of 250kN. When the same is tested as a strut with both ends hinged 2m long, it failed at a load of 150kN. Find the value of constant ‘α’ in Rankine’s formula. (AUC Apr/May 2012)
11. Derive an expression for crippling load when one end of the column is fixed and the other end is free.
12. Calculate the Euler’s critical load for a strut of T-section. The flange width being 10cm, overall depth 8cm and both flange and stem 1cm thick. The strut is 3m long and is built in at both ends. Take E = 2 x 105 N/mm2.
13. Derive Euler’s crippling load for the following cases:
i. Both ends hinged. (8m)
ii. One end is fixed and other end free (8m)
13. A column with one end hinged and other end fixed has a length of 5m and a hollow circular cross-section of outer dia 100mm and wall thickness 10mm. If E = 1.60 x 105
N/mm2 and crushing stress σc= 350 N/mm2, find the load that the column may carry with
a factor of safety of 2.5 according to Euler theory and Rankine-Gordon theory.
14. i. Derive an expression for the bucking load of a column hinged at both ends. (8m)
ii. A hollow cast iron column whose outside diameter is 200mm has a thickness of
20mm. It is 4.5m long and is fixed at both ends. Calculate the safe load by Rankine- Gordon formula using a factor of safety 4. (8m)
15. A pipe of 200mm internal diameter and 50mm thickness carries a fluid at a pressure of
10 MN/m2. Calculate the maximum and minimum intensities of circumferential stress across the section. Also sketch the radial and circumferential stress distribution across the section.
16. A 2m long pin ended column of square cross section is to be made of wood. Assuming E
=12 GPa and allowable stress being limited to 12 MPa, determine the size of the column to support the following loads safely. (i) 95 KN (ii) 200 KN. Use factor of safety of 3 and also calculates the Euler’s crippling load for buckling.
17. Determine the buckling load for a column of T section with flange of 100mm width and overall depth 120mm. Both flange and web are of 10mm thick. The strut is 3m long with one end hinged and other end fixed.
18. Determine the buckling load for a column of rectangular section of size 100mm width and overall depth 120mm. The strut is 3m long with one end hinged and other end fixed.
19. A compound cylinder is made by shrinking a cylinder of external diameter 300mm and internal diameter 250mm over another cylinder of external diameter 250mm and internal diameter 200mm. The radial pressure at the junction is 8 N/mm2. Find the final stresses set up across the section when the compound cylinder is subjected to an internal pressure of 84.5 N/mm2.
20. i) A hollow mild steel tube 6m long 4 cm internal diameter and 6mm thick is used as a strut with both ends hinged. Find the buckling load and safe load taking factor of safety
3. E = 200 GPa. (8m)
ii) Find the Euler buckling load for a fixed-fixed column. (8m
UNIT – IV - STATE OF STRESS IN THREE DIMENSIONS
PART – A (2 Marks)
| 1. | Define principal plane and principal stress. | (AUC Apr/May 2010 & Apr/May 2011) | |
| 2. | State the principal stress theory of failure. | (AUC Apr/May 2010 & 2012) | |
| 3. | Define volumetric strain. | (AUC Nov/Dec 2010) | |
| 4. | What are principal stresses and principal planes? | (AUC Nov/Dec 2010) | |
| 5. | State distortion energy theory of failure. | (AUC Apr/May 2011) | |
| 6. | State the maximum principal stress theory. | (AUC Nov/Dec 2011) | |
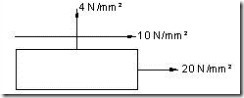
| 7. | For the state of stress shown in fig. identify the principal planes. | (AUC Nov/Dec 2011) | |
8. What is deviatric component of a stress tensor? (AUC Apr/May 2012)
9. What is meant by stress tensor?
10. State principal strain theory.
11. What will be the fixed end moment for a beam subjected to uniformly varying load, which is maximum at the centre and minimum at supports?
12. State maximum principal strain theory.
13. List the theories of failure.
14. What is stress invariant?
15. What do you mean by triaxial state of stress?
16. What is meant by principal plane?
17. Find the principal stresses if the normal stresses σx and σy and shear stress τ act at a
point?
PART – B (16 Marks)
1. i) Briefly explain spherical and deviatory components of stress tensor. ii) Explain the importance of theories of failure.
iii) For the state of stress shown in Fig, find the principal plane and principal stress.
(AUC Apr/May 2010)
2. A circular shaft has to take a bending moment of 9000 N/m and torque 6750 N/m. The stress at elastic limit of the material is 207 × 106 N/m2 both in tension and compression. E = 207 x 106 KPa and µ = 0.25.Determine the diameter of the shaft, using octahedral shear stress theory and the maximum shear stress theory. Factor of safety : 2.
(AUC Apr/May 2010)
3. i) State Maximum Shear Stress Theory
ii) A shaft is subjected to a maximum torque of l0 kNm and a maximum of bending moment of 8kNm at a particular section. If the allowable equivalent stress in simple tension is 160MN/m2, find the diameter of the shaft according to the maximum shear stress theory. (AUC Nov/Dec 2010)
4. In a steel member, at a point the major principal stress is 200MN/m2 and the minor principal stress is compressive. If the tensile yield point of the steel is 235MN/m2, find the value of the minor principal stress at which yielding will commence, according to each of the following criteria of failure
i) Maximum shearing stress.
ii) Maximum total strain energy and
iii) Maximum shear strain energy. Take Poisson Ratio = 0.26. (AUC Nov/Dec 2010)
5. The rectangular stress components of a point in three dimensional stress system are
defined as σ x = 20 MPa , σ y = -40 MPa , σ z = 80 MPa ,t xy = 40 MPa ,
t yz = -60 MPa and
t zx = 20 MPa . Determine the principal stresses at the given point. (AUC Apr/May 2011)
6. A steel shaft is subjected to an end thrust producing a stress of 90 MPa and the maximum shearing stress on the surface arising from torsion is 60 MPa. The yield point of the material in simple tension was found to be 300 MPa. Calculate the factor of safety of the shaft according to (i) Maximum shear stress theory and (ii) Maximum distortion energy theory. (AUC Apr/May 2011)
7. i) State the shear strain energy theory and a comment on it.
ii) For the state of stress shown in fig. find the principal plane, principal stress and maximum shear stress. (AUC Nov/Dec 2011)
8. In a material the principal stresses are 50 N/mm2, 40 N/mm2 and – 30 N/mm2. Calculate the total strain energy, volumetric strain energy, shear strain energy and factor of safety on the total strain energy criterion if the material yields at 100 N/mm2.
(AUC Nov/Dec 2011)
9. The state of stress at a point is given by the tensor below. Determine the principal
æ 20 -10 -30 ö
|
è -30 20 -20 ø
MPa. (AUC Apr/May 2012)
10. Explain any two theories of failure. (AUC Apr/May 2012)
11. The normal stress in two mutually perpendicular directions are 600 N/mm2 and 300
N/mm2 both tensile. The complimentary shear stresses in these directions are of intensity
450 N/mm2. Find the normal and tangential stresses in the planes which are equally inclined to the planes carrying the normal stresses mentioned above.
12. A solid circular shaft is subjected to a bending moment of 40 kN m and a torque of 10 kN
m. Design the diameter of the shaft according to i. Maximum principal stress theory
ii. Maximum shear stress theory iii. Maximum strain energy theory.
11. Two mutually perpendicular planes of an element of a material are subjected to direct stresses of 10.5 MN/m2 (tensile); and 3.5 MN/m2 (compressive) and shear stress of 7
MN/m2. Find
i. The magnitude and direction of principal stresses. (12m)
ii. The magnitude of the normal and shear stresses on a plane on which the shear stress is maximum. (4m)
12. Derive the expressions for energy of distortion and energy of dilatation?
æ 9 6 3 ö
|
è 3 2 4 ø
ii. Determine the principal stresses. (8m)
14. A cylindrical shell 1.2m diameter is to be made of mild steel plates. It is subjected to an internal pressure of 1.5 MN/m2. If the material yields at 200 kN/m2, calculate the thickness of the plate on the basis of following theories of failure assuming a FOS of 3 in each case.
i. Maximum principal stress theory ii. Maximum shear stress theory
iii. Maximum shear strain energy theory.
15. Determine the principal moments of inertia for an angle section 80 mm x 80 mm x10 mm.
16. Find the principal stresses and principal planes for the following 3D stress field.
|
è 20 30 40 ø
17. A thick cylinder pressure vessel of inner radius 150mm is subjected to an internal pressure of 80 MPa. Calculate the wall thickness based upon
i. Maximum principal stress theory ii. Total strain energy theory.
Take Poisson’s ratio = 0.3 and yield stress = 300 MPa.
UNIT – V - ADVANCED TOPICS IN BENDING OF BEAMS
PART – A (2 Marks)
1. What is ‘fatigue strength’ and ‘endurance ratio’ in a fatigue testing of material?
(AUC Apr/May 2010)
2. Write the Winkler-Bach formula for a curved beam. (AUC Apr/May 2010)
3. Distinguish between symmetrical and unsymmetrical sections of beams.
(AUC Nov/Dec 2010)
4. What are the causes of fatigue in beams? (AUC Nov/Dec 2010)
5. What are the reasons for unsymmetrical bending? (AUC Apr/May 2011)
6. Write the expression for position of neutral axis in case of curved bars.
(AUC Apr/May 2011)
7. What is stress concentration? (AUC Nov/Dec 2011)
8. For the phase section shown in fig. find the product moment of inertia about x and y
axes. (AUC Nov/Dec 2011)
9. Define: Shear centre. (AUC Apr/May 2012)
10. State Winkler Bach formula. (AUC Apr/May 2012)
11. Define ‘Fatigue’.
12. What are the reasons for unsymmetrical bending?
13. What are the assumptions made in Winkler – Bach theory?
14. What is stress concentration?
15. Define: fatigue life and endurance ratio.
16. How would you find the bending stress in unsymmetrical section?
17. State any four assumptions made in the analysis of stresses in curved bars.
18. When will you use the simple flexure formula for curved beams?
19. What do you mean by unsymmetrical bending?
PART – B (16 Marks)
1. A rectangular simply supported beam is shown in Fig. The plane of loading makes30° with the vertical plane of symmetry. Find the direction of neutral axis and the bending stress at A. (AUC Apr/May 2010)
2. A curved bar of rectangular section, initially unstressed is subjected to bending moment of 2000 N.m tends to straighten the bar. The section is 5 cm wide and 6 cm deep in the plane of bending and the mean radius of curvature is 10 m. find the position of neutral axis and the stress at the inner and outer face. (AUC Apr/May 2010)
3. A thick cylinder of external and internal diameter of 350 mm and 200 mm is subjected to an internal pressure of 45 N/mm2 and external pressure 5N/mm2. Determine the stress in the material. Now if the external pressure is doubled, what internal pressure can be maintained without exceeding the previously determine maximum stress?
(AUC Nov/Dec 2010)
4. Write brief technical note on:
i) Unsymmetrical bending of beams ii) Curved beams
iii) Stress concentration
iv) Significance of shear centre. (AUC Nov/Dec 2010)
5. A 80 × 80 × 10 mm angle is used as a simply supported beam over a span of 2.4m. It carries a load of 400kN along the vertical axis passing through the centroid of the section. Determine the resulting bending stress on the outer corners of the section along the middle section of the beam. (AUC Apr/May 2011)
6. A central horizontal section of hook is a symmetrical trapezium 60 mm deep, the inner width being 60mm and the outer being 30 mm. Estimate the extreme intensities of stress when the hook carries a load of 30 kN, the load line passing 40mm from the inside edge of the section and the centre of curvature being in the load line. (AUC Apr/May 2011)
7. Fig. shows a frame subjected to a load of 3.4 kN find the resultant stress at A and B. (AUC Nov/Dec 2011)
8. A beam of T-section (flange: 100 × 20 mm, web: 150 mm × 10 mm) in 3 m in length and simply supported at ends (Fig). It carries a load of 2.2 kN inclined 20° to the vertical and passing through the centroid of the section. Calculate the maximum tensile stress and maximum compressive stress. Also find the position of the neutral axis. (AUC Nov/Dec 2011)
9. Determine the shear centre for a channel section shown in fig. (AUC Apr/May 2012)
10. Find the centroidal principal moments of inertia of an angle section 300mm x 200mm x 20mm as shown in fig. (AUC Apr/May 2012)
11. A curved bar is formed of a tube of 120 mm outside diameter and 7.5 mm thickness. The centre line of this beam is a circular are of radius 225 mm. A bending moment of 3 kN m tending to increase curvature of the bar is applied. Calculate the maximum tensile and compressive stresses set up in the bar.
12. A 80 mm x 80 mm x 10mm angle section shown in fig is used as a simply supported beam over a span 2.4 m. It carries a load of 400 N along the line YG, where G is the centroid of the section. Calculate the i. Stresses at the points A, B and C of the mid section of the beam
ii. Deflection of the beam at the mid section and its direction with the load line iii. Position of the neutral axis. Take E = 200 GN/m2.
13. Determine the principal moments of inertia for an angle section 80mm x 80mm x 10mm.
14. A curved bar is formed of a tube of 120mm outside diameter and 7.5mm thickness. The centre line of this beam is a circular arc of radius 225mm. A bending moment of 3 kNm tending to increase curvature of the bar is applied. Calculation the maximum tensile and compressive stresses set up in the bar.
15. A 40mm x 40mm x 5mm angle is used as a simply supported beam over a span of 2.4m. It carries a load of 200N along vertical axis passing through the centroid of the section. Determine the resulting bending stress on the outer corners of the section, along the middle section of the beam.
16. At the critical section of a crane hook, trapezium in section, the inner and outer sides are 4cm and 2.5cm respectively and depth is 7.5cm. The centre of curvature of the section is at a distance of 6cm from the inner fibers. If the maximum stress is not to exceed 120 MN/m2, what maximum load the hook can carry?
17. A curved bar is formed of a tube of 120 mm outside diameter and 7.5 mm thickness. The centre line of this beam is a circular arc of radius 225 mm. A bending moment of 3 kNm tending to increase curvature of the bar is applied. Calculate the maximum tensile and compressive stresses set up in the bar.
18. Determine the horizontal and vertical deflection of the end B of the thin curved beam shown in fig. Take E = 200 GN/m2, width and thickness of the beam 10 mm and 5 mm respectively. P = 2 N.