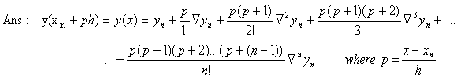Electromagnetic Fields–April / May 2010 Question Paper

Anna University

B.E./B.Tech. DEGREE EXAMINATION, APRIL/MAY 2010

Fourth Semester

Electronics and Communication Engineering

---

EC2253 — ELECTROMAGNETIC FIELDS

(Regulation 2008)

---

Time: Three hours

Maximum: 100 Marks

---

Answer ALL Questions

PART A — (10 x 2 = 20 Marks)

1. State Stoke’s theorem.

2. Define electric scalar potential.

3. State Biot-Savart law.

4. Write down Lorentz force equation.

5. Define dielectric strength of material and give its unit.

6. What do you mean by Magnetization?

7. What is Displacement current density?

8. State Poynting vector.

9. What is skin effect?

10. Define Brewster angle.

---

Part B – (5 X 16 = 80)

Download from the Below Link to view the Full Question Paper.

---

Download :

• EMF-Aprl-may-2010.pdf (100kb)

---

Control System–16marks Important Questions

Anna University

CONTROL SYSTEM

16marks IMPORTANT QUESTIONS

Recommended For EEE Department

Semester 4

---

UNIT 1

1. Explain the TF of armature and field controlled DC motor. (16)

2. Problem from mechanical translational system(analogy of force- voltage and force- current) (16)

3. Problem from signal flow graph + block diagram (8 +8 )

---

Unit 2

1. Explain servomotors and its types (16)

2. Derive the time response of underdamped and critically damped second order system for unit step input (16)

3. Derive the expression for time domain specifications (16)

---

Unit 3

1. Derive the frequency domain specifications of second order system (16)

2. Problem from bode plot determining phase margin,gain margin ,determination of k value,gain and phase cross over frequency( any 2 ) (16)

3. Problem from polar plot (same as bode plot )(16)

4. Explain frequency domain specifications (8)

---

Unit-4

1. Explain the locatiuon of poles on s-plane for stability (16)

2. Problems from routh Hurwitz criterion (8)

3. Problems to determine gain and phase cross over frequency, gain and phase margin from given TF (16)

4. Problems from root locus (16)

---

Unit – 5

1. Derive the realisation of electrical network, frequency response, determination of maximum phase lag and max. Lag angle for

a) lag compensator (16)

b) lead compensator (16) (separate questions)

2. problems from lag compensator or lead compensator (each 16 marks )

---

PROBABILITY & RANDOM PROCESS Question Bank

Anna University

Department of Electronics and Communication Engineering

PROBABILITY & RANDOM PROCESS Question Bank

SUBJECT CODE : 181403

SUBJECT NAME : PROBABILITY & RANDOM PROCESS

BRANCH / YEAR : ECE / II

Content :
Includes all units Important Question's (2marks and 16marks)

Download :
PRP-QB.pdf (2.3 mb) 

LINEAR INTEGRATED CIRCUITS (LIC)–April / May 2010 Question Paper

Anna University

B.E./B.Tech. DEGREE EXAMINATION, APRIL/MAY 2010

Fourth Semester

Electronics and Communication Engineering

EC2254 — LINEAR INTEGRATED CIRCUITS

(Regulation 2008)

---

Time: Three hours Maximum: 100 Marks

Answer ALL Questions

---

PART A — (10 × 2 = 20 Marks)

1. What is an integrated circuit?

2. What is current mirror?

3. Give the schematic of op-amp based current to voltage converter.

4. Draw the circuit diagram of differentiator and give its output equation.

5. What is a VCO?

6. Draw the relation between the capture ranges and lock range in a PLL.

7. Define resolution of a data converter.

8. Give the advantages of integrating type ADC.

9. Draw the internal circuit for audio power amplifier.

10. What are the three different wave forms generated by ICL8038?

---

PART B — (5 × 16 = 80 Marks)

11. (a) (i) Define CMRR. Draw the circuit of an Op-amp differential amplifier and give the expression for CMRR. (8)

(ii) Define Slew Rate. Explain the cause of slew rate and derive an expression for Slew rate for an op-amp voltage follower. (8)

Or

(b) Briefly explain the various processes involved in fabricating monolithic IC which integrates bipolar transistor, diode, capacitor and resistor. (16)

---

12. (a) (i) Design a first order Low-pass filter for cut-off frequency of 2 KHz and pass-band gain of 2. (8)

(ii) Explain a positive clipper circuit using an Op-amp and a diode with neat diagrams. (8)

Or

(b) (i) Design a circuit to implement V0 = 0.545V3 + 0.273V4 −1.25V1 − 2V2 . (8)

(ii) Draw and explain a simple Op-amp differentiator. Mention its limitations. Explain with a neat diagram how it can be overcome in a practical differentiator. Design an Op-amp differentiator that will differentiate an input signal with maximum frequency f max =100 Hz . (8)

---

13. (a) (i) With a neat diagram explain the variable transconductance

technique in analog multiplier and give its output equation. (8)

(ii) Briefly explain the working of voltage controlled oscillator. (8)

Or

(b) What are important building block of phase locked loop ( PLL) explain its Working? (16)

---

14. (a) (i) Explain the working of R-2R ladder DAC. (8)

(ii) Explain the working of success approximation ADC. (8)

Or

(b) (i) A dual slope ABC uses a 16-bit counter and a 4 MHz clock rate. The maximum input voltage is +10V. The maximum integrator output voltage should be -8V when the counter has recycled through 2n counts. The capacitor used in the integrator is 0.1µF . Find the value of resistor R of the integrator. (8)

(ii) What is a sample and hold circuit? Briefly explain its construction and application. (8)

---

15. (a) (i) How is voltage regulators classified? Explain a series voltage regulator. (8)

(ii) What is an optocoupler? Briefly explain its characteristics. (8)

Or

(b) With a neat circuit diagram and internal functional diagram explain the working of 555 timers in astable mode. (16)

---

Communication Theory–April / May 2010 Question Paper

Anna University

B.E./B.Tech.Degree Examinations,Apr/May 2010

---

Regulations 2008

Fourth Semester

Electronics and Communication Engineering

EC2252 Communication Theory

---

Time: Three Hours

Maximum: 100 Marks

Answer ALL Questions

Part A - (10 x 2 = 20 Marks)

1. How many AM broadcast stations can be accommodated i n a 100 kHz bandwidth if t he highest frequency modulating a carrier i s 5 kHz?

2. What are the causes of linear distortion?

3. Draw t he block diagram of a method for generating a narrowband FM signal.

4. A carrier wave of frequency 100 MHz i s frequency modulated by a signal 20 sin(200π × 103t).

What i s bandwidth of FM signal if the frequency sensitivity of t he modulation is 25kH z/V .

5. When i s a random process called deterministic?

6. A receiver connected to a n antenna of resistance of 50Ω has an equivalent noise resistance of 30Ω. Find the receiver noise figure.

7. What are t he characteristics of super heterodyne receivers?

8. What a re the methods to improve FM threshold reduction?

9. Define entropy function.

10. Define Rate Bandwidth an d Bandwidth efficiency.

---

Part B - (5 x 16 = 80 Marks)

11. (a) (i) Draw an envelope detector circuit used for demodulation of AM an d ex- plain its operation. (10)

(ii) How SSB can be generated using Weaver’s method? Illustrate with a neat block diagram. (6)

OR

11. (b) (i) Discuss i n detail about frequency translation and frequency division multiplexing technique with diagrams. (10)

(ii) Compare Amplitude Modulation and Frequency Modulation. (6)

12. (a) (i) Using suitable Mathematical analysis show that FM modulation produces infinite sideband. Also deduce an expression for the frequency modulated output and its frequency spectrum. (10)

(ii) How can you generate an FM from PM and PM from FM? (6)

OR

12. (b) (i) A 20 MHz i s frequency modulated by a sinusoidal signal such that t he maximum frequency deviation is 100 kHz. Determine the modulation index and approximate bandwidth of t he FM signal for t he following modulating signal frequencies,

(1) 1 kHz (2) 100 kHz and (3) 500 kHz. (8)

(ii) Derive the time domain expressions of FM and PM signals. (8)

13. (a) (i) Give a random process, X (t) = A cos(ωt + θ), where A an d ω a re constants and θ i s a uniform random variable. Show that X (t) is ergodic in both mean and autocorrelation. (8)

(ii) Write a short note on shot noise and also explain about power spectral density of shot noise. (8)

OR

13. (b) Write t he details about narrow band noise and t he properties of quadrature components of narrowband noise. (16)

14. (a) Derive a n expression for SNR at input (SNRc ) and output of (SNRo) of a coherent detector. (16)

OR

14. (b) (i) Explain pre-emphasis and De-emphasis i n detail. (10)

(ii) Compare the performances of AM and FM systems. (6)

15. (a) (i) Find the code words for five symbols of t he alphabet of a discrete memory- less source with probability {0.4, 0.2, 0.2, 0.1, 0.1}, using Huffman coding and determine the source entropy and average code word length. (10)

(ii) Discuss the source coding theorem. (6)

OR

15. (b) (i) Derive t he channel capacity of a continuous band limited white Gaussian noise channel. (10)

(ii) Discuss about rate distortion theory. (6)

COMMUNICATION THEORY - May / June 2009 Question Paper

Anna University

B.E / B.Tech. DEGREE EXAMINATION, MAY/JUNE 2009.

Fifth Semester

Electronics and Communication Engineering 

EC 1301— COMMUNICATION THEORY 

(Regulation 2004)

(Common to B.E. (Part-Time) Fourth Semester — Regulation 2005)

Time : Three hours

Maximum: 100 marks

Answer ALL questions.

PART A  -(10 x 2 = 20 marks)

1. Compute the bandwidth of the Amplitude Modulated signal

2. In a Superheterodyne Receiver used for AM demodulation, the If frequency is 455 KHz. If it is required to receive an AM signal centred around 1050 KHz and bandwidth 10 KHz, give the characteristics of the Image rejectionfilter for a suitable choice of Local oscillator frequency.

3. Obtain the bandwidth of the FM signal

4. What do you understand by FM stereo multiplexing? .

5. A white noise has a power spectral density of —170 dBm/Hz. Calculate the
power at the output of a Band Pass Filter of center frequency 120 MHz and
bandwidth 20 KHz if white noise is fed as the input.

6. Give the characteristics of Shol Noise.

7. Compare the noise performance of AM and FM systems.8. What is threshold effect in FM?

9. Calculate the entropy of the source if the symbol set is (s ,s2,s3,s4 J and the corresponding probabilities are (0.2,0.3,0.05,0.45).

10. State Channel coding theorem.

PART B - (5x16=80marks)

11. (a) Give the method for generation of AM, DSBSC and SSB waves. (16)

Or

(b) (i) Discuss the operation of Costas Loop in detail. (8)

(ii) Draw the block diagram for FDM and explain. (8)

12. (a) Discuss on FM demodulation using PLL. (16)

Or

(b) (i) Give the method of Generàtion of FM signal. (6)

(ii) Derive the expression for the spectrum of a FM signal with single
tone modulation. (10)

13. (a) Give the detailed noise analysis of a SSB receiver using coherent
detection. (16)

Or

(b) Define Narrow b

and noise. List the properties of narrow band noise and 

give a brief explanation of each of them. (16)

14. (a) Derive the expression for the Power spectral density at the output of a FM discriminator when the received signai is corrupted by additive white Gaussian Noise. (16)

Or

(b) (i) Discuss Pre-emphasis and De-emphasis in FM. (6)

(ii) Discuss the threshold effect in an envelope detector used in an AM receiver. (10)

15. (a) Discuss the various techniques used for compression of information. (16)

Or

(b) (i) Define Differential entropy. (2)

(ii) Define Mutual Information. (2)
(iii) What is the relation between Mutual Information and Channel
Capacity? - (1)
(iv) Give the (Shannon-Hartley) information capacity theorem and
discuss the implication of the same in detail. (11)

Numerical Methods–Unit 2–2 Marks with Answers

Anna University

Numerical Methods

---

UNIT-II

INTERPOLATION AND APPROXIMATIONT

Two Marks With Answers

---

1. Explain briefly Interpolation.

Ans: Interpolation is the process of computing the values of a function for any value of the independent variable within an interval for which some values are given.

---

2. Definition of Interpolation and extrapolation.

Ans: Interpolation: It is the process of finding the intermediate values of a function from a set of its values specific points given in a tabulated form. The process of computing y corresponding to x is interpolation.

Extrapolation: If then the process is called extrapolation.

---

3. State Newton’s Forward interpolation formula.

---

4. State Newton’s Backward interpolation formula.

---

5. Error in Newton’s forward:

---

6. Error in Newton’s Backward:

---

7. State Newton’s divided difference formula.

---

8. Show that the divided differences are symmetrical in their arguments.

---

9. Show that divided difference operator is linear.

Ans: [f(x)g(x)] =

= = f(x) g(x).

---

10. Divided difference table:

X	Y	Y	2 Y	3Y
X0 X1 X2 X3	Y0 Y1 Y2 Y3

---

11. Write Lagrangian’s polynomial formula.

---

12. What is the assumption we make when Lagrange’s formula is used?

Ans: It can be used whether the values of x, the independent variable are equally spaced or not whether the difference of y become smaller or not.

---

13. Write Lagrangian inverse interpolation formula.

---

14. Define Cubic Spline

Ans: Let , i = 0, 1, 2... n be the given (n +1) pairs of a data. The third order curves employed to connect each pair of data points are called cubic splines. (OR) A smooth polynomial curve is known as cubic spline.

A cubic spline function f(x) w.r.t. the points x₀, x_{1, .....}x_n is a polynomial of degree three in each interval (x_i-1, x_i) i = 1, 2, ...n such that , and are continuous.

---

15. Write down the formula of Cubic Spline.

and

where M =

(OR)

where and ; i = 1,2,3,....

---

Numerical Methods–Unit 1 Two Marks with Answers

Anna University

NUMERICAL METHODS

---

UNIT-I

SOLUTION OF EQUATIONS AND EIGENVALUE PROBLEMS

Two Marks with Answes

---

1. If a function f(x) = 0 is continuous in the interval (a, b) and if f (a) and f (b) are of opposite signs. Then one of the root lies between a and b.

---

2. Example of Algebraic equation:

(i) x³ – 2x + 5 = 0;

(ii) 2x³ – 3x – 6 = 0.

---

3. Example of Transcendental equation:

(i) x – cosx = 0;

(ii) xe^x -2 = 0;

(iii)

---

4. Regula Falsi Method:

 

(First iteration of Regula Falsi Method).

---

5. Iterative Method:

.

---

---

6. Convergence condition of iterative method is

.

---

---

7. Order of convergence of iterative method is linear (i.e.) 1.

---

8. Newton Raphson’s Method (Method of Tangents):

=.

---

9. Convergence condition of N-R method is

 

---

10. Order of convergence of Newton’s method is quadratic (i.e.) 2.

11. Direct Method:

(i) Gauss Elimination Method,

(ii) Gauss Jordan Method.

---

12. Indirect Method (or) Iteration Method:

(i) Gauss-Jacobi Method,

(ii) Gauss-Seidel Method.

---

13. Gauss Elimination Method: To reduce the augmented matrix [A, B] to upper triangular matrix. Then, using Back Substitution method we’ve to find the unknowns.

---

14. Gauss Jordan Method: To reduce the augmented matrix [A, B] to diagonal matrix. Finally this system of equation each has only one unknown and then we’ve to find the unknowns directly.

---

15. Diagonally Dominant: An nn matrix A is said to be diagonally dominant if the absolute value of each leading diagonal element is greater than or equal to the sum of the absolute values of the remaining elements in that row.

Given system of equations is

;;

is a diagonal system is if

---

16. Gauss Jacobi Method: If the given system of equation is diagonally dominant then

 

---

17. Gauss Seidel Method: If the given system of equation is diagonally dominant then

 

---

18. Sufficient condition for iterative methods (Gauss Seidel Method & Gauss Jacobi Method) to convergence is the coefficient matrix should be diagonally dominant.

---

19. The iteration method is a self correcting method since the round off error is smaller.

---

20. Why Gauss Seidel iteration is a method of successive corrections?

Ans: Because we replace approximations by corresponding new ones as soon the latter have been computed.

---

21. Compare Gauss Elimination Method and Gauss Jordan Method

Gauss Elimination Method	Gauss Jordan Method
1. Direct Method 2. Coefficient matrix is transformed into upper triangular matrix. 3. We obtain the solution by back substitution method.	1. Direct Method 2. Coefficient matrix is transformed into diagonal matrix. 3. No need of back substitution method. Since finally this system of equation each has only one unknown.

---

22. Inverse of a Matrix: Let A be an nn nonsingular matrix. If X is the inverse of the matrix A then AX = I (i.e.) X = I A^-1. We start with augmented matrix of A with identity matrix I of the same order and convert A into the required form (i.e.) identity then the inverse is formed. [A / I ] [I / A^-1].

---

23. Compare Gauss Elimination Method and Gauss Seidel Method.

Gauss Elimination Method	Gauss Seidel Method
1. Direct Method 2. It has the advantage that it is finite and works in theory for any non-singular set of equation. 3. We obtain exact value.	1. Indirect Method 2. It converges only for diagonally dominant. 3. Approximate value which is self correct method.

---

24. Compare Gauss Jacobi and Gauss Seidel Methods.

Gauss Jacobi Method	Gauss Seidel Method
1. Indirect Method 2. Convergence rate is slow. 3. Condition for convergence is diagonally dominant.	1. Indirect Method 2. The rate of convergence of this method is roughly twice that of Jacobi. 3. Condition for convergence is diagonally dominant.

---

25. Why Gauss Seidel method is better method than Jacobi’s method?

Ans: Since the current value of the unknowns at each stage of iteration are used in proceeding to the next stage of iteration, the convergence in Gauss Seidel method will be more rapid than in Gauss Jacobi method.

---