Divergence Theorem
The volume
integral of the divergence of a vector field over a volume is equal to the
surface integral of the normal component of this vector over the surface
bounding the volume.
Proof:
The divergence of any
vector A is given by:
Take the volume
integral on both sides
Since dv = dx dy dz
Consider an element
volume in x direction.
But,
Substitute Equation 4 in Equation 3:
Where dy dz = dsx
= x component of surface area ds.
Similarly the following
integrands become:
Then, Substitute in
Equation 2:
Hence Divergence Theorem Proved !!






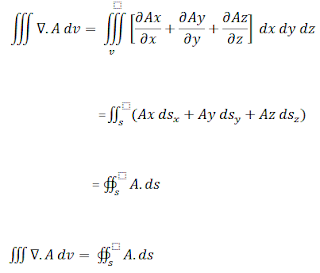





No comments:
Post a Comment